Some Properties of the Orthic Triangle - Conics

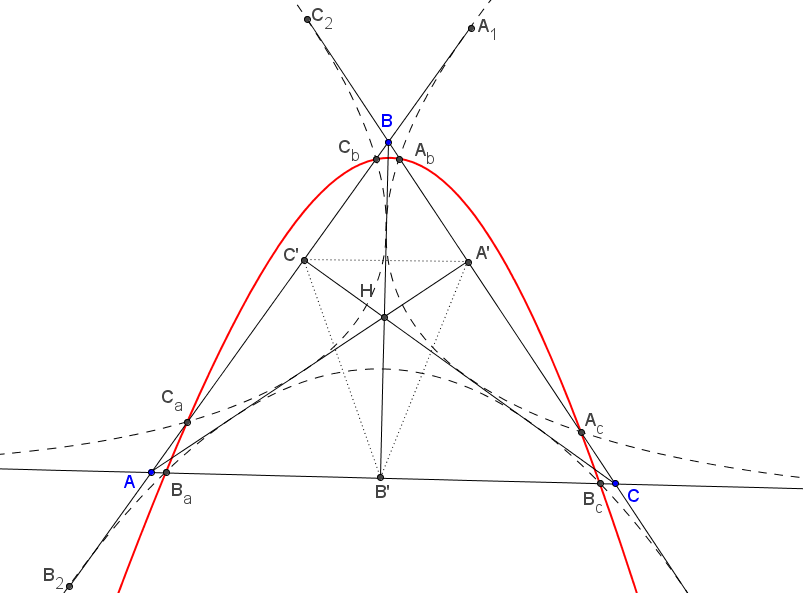
Let $ABC$ be a triangle. Let $A'B'C'$ be the orthic triangle of $ABC$. Draw a parabola focus at $A'$, directrix $B'C'$. Then, the parabola touches $BB'$ in $T_b$, $CC'$ in $T_c$, $AB$ in $A_1$ and $AC$ in $A_2$.

Proof:


Consider the following configuration:

Now it is easy to see why $BB'$, $CC'$ are tangent to the parabola.

We know that the orthocenter of $ABC$ is the incenter of the orthic triangle $A'B'C'$. 

The tangency of $AB$ and $AC$ with the parabola follows directly from the Orthoptic property.

Addendum:

*Define $B_1$, $B_2$, $C_1$, $C_2$ as we define $A_1$, $A_2$.

Then, $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$ lie on a conic.

**Let the parabola cut the side $BC$ in $A_b$, $A_c$. Define $B_a$, $B_c$, $C_a$, $C_b$ cyclically. Then, these six points also lie on a conic.

Proof