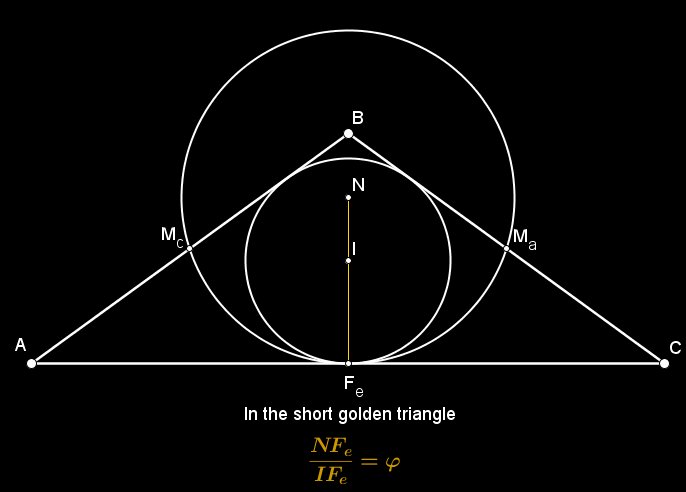
Proposition $1$. Let $ABC$ be a short golden triangle $(108°-36°-36°)$. Call $H$ the orthocenter of $\triangle{ABC}$ and let $h_ah_bh_c$ be the orthic triangle of $\triangle{ABC}$. Let $T_a$ be the point where the incircle of $\triangle{ABC}$ touch $BC$ and $M_a$ the midpoint of side $BC$. The parabola with focus at $h_c$ and directrix $h_ah_b$ is tangential to side $BC$ at $D$ (for a proof, see $[1]$), where $$\frac{M_aD}{DT_a}= \phi$$
Proof. From the definition of parabola $Dh_c = DF$ and $DF\perp h_ah_b$. As $\triangle{h_ah_bh_c}$ is the orthic triangle of $\triangle{ACH}$, from theorem $2$ it follows $\angle{h_ch_aD} = \angle{Dh_aF}$. $Sin \angle{h_ch_aD} = sin\angle{Dh_aF} = \frac{DF}{Dh_a}$. From the Law of Sines, $\frac{Dh_a}{sin\angle{Dh_ch_a}}= \frac{Dh_c}{sin\angle{Dh_aF}}$; $\frac{Dh_a}{sin\angle{Dh_ch_a}}= \frac{Dh_c}{\frac{DF}{Dh_a}}$; $sin\angle{Dh_ch_a}= \frac{DF}{Dh_c}$. But $Dh_c = DF$, hence, $sin\angle{Dh_ch_a} = 1$ and $\angle{Dh_ch_a}$ is right. Since $DFh_ah_c$ is a kite with two right-triangles, $D$, $F$, $h_a$, $h_c$ are cyclic.
Lemma $4$. $\triangle{ABC}$ ∼ $\triangle{DFh_c}$.
Proof. Clearly, $CHh_ah_b$ is cyclic. Consider the right triangle $ACh_c$. $\angle{CHh_b} = 90^\circ - 54^\circ = 36^\circ$. From property of inscribed angle, $\angle{CHh_b}=\angle{Ch_ah_b}=\angle{Ch_aF}$. From lemma $3$ we know that $DFh_ah_c$ is cyclic, so $\angle{Dh_cF}=\angle{Dh_aF}=36^\circ$. As $\triangle{DFh_c}$ is isosceles with $Dh_c = DF$, it follows that $\triangle{ABC}$ ∼ $\triangle{DFh_c}$, as desired.
Proof. $IT_a = Ih_b = r$. $\angle{T_ah_bH}=\frac{180^\circ-\angle{T_aIh_b}}{2}=\frac{180^\circ-144^\circ}{2}=18^\circ$. Note that $\angle{HCh_a} = \angle{Hh_bh_a} = \angle{Hh_bh_c} = 18^\circ$. It follows that $\angle{T_ah_bH} = \angle{Hh_bh_c}$, which means $h_b$, $T_a$, $h_c$ are collinear.
Back to the main result.
By simple angle chasing $\triangle{Bh_cT_a}$, $\triangle{Bh_cM_a}$ are both tall golden triangles and $\triangle{h_cM_aT_a}$ is a short golden triangle. $Dh_c$ is the angle bisector of $\angle{M_ah_cT_a}$ and we know $\frac{h_cM_a}{h_cT_a}=\phi$ (this is a well-known property of the short golden triangle) and by the Angle Bisector theorem $\frac{M_aD}{DT_a}=\phi$ , as desired.