domingo, 28 de diciembre de 2014
domingo, 21 de diciembre de 2014
Concurrence On The Nine-Point Circle (No proven yet)
Much more interesting than the particular case I proposed, is the generalization by Francisco Javier García Capitán at ADGEOM1280.
Given a triangle ABC and a point P. Call A1B1C1 be the circumcevian triangle of the complement of P with respect the medial triangle. Call A2B2C2 the triangle formed by the reflections of the vertices of the pedal triangle of P on the center of the pedal circle of P, that is the antipodes of the vertices of the pedal triangle on its circumcircle. The triangles A1B1C1 and A2B2C2 are perspective at a point Q on the nine point circle.
sábado, 20 de diciembre de 2014
Pólya on Mathematical Abilities.
Pólya interviewed by Jeremy Kilpatrick.
JK: How did you identify the students you had who were best in mathematics? You taught some students who were good in mathematics. How could you tell who were the best ones?
GP: Who was the best one, I can’t tell you.
JK: Well, among the best, how could you identify their talent? They were quicker?
GP: Anyhow, they asked good questions. So they found out something by themselves. And so on. There is no simple way—. You see, people are too different. Mathematicians are too different. There is no simple way of describing it. I don’t think so.
JK: What about people who are creative in mathematics as opposed to just being able to learn it? What does that take? What does that require? Just great interest?
GP: I don’t know.
JK: Not everyone could be creative in mathematics.
GP: I said somewhere, “What is the difference between productive and creative?” If you think about a problem, if you produce a result, then you are productive. If in working you get into a method with which you can solve also other problems, then you are creative. That’s the difference. And that is difficult to say. I don’t think there are obvious signs to recognize this. I don’t think so.
martes, 16 de diciembre de 2014
viernes, 3 de octubre de 2014
Circle and Lucas Cubic
This is a generalization of proposition 2 in my paper A Note on Reflections.
On June, 10, 2014, I posed a problem at ADGEOM, which was generalized by Angel Montesdeoca in the following form:
Let ABC be a triangle. Let P be an arbitrary point on the plane of ABC. Reflect P around the vertices of cevian triangle X_aX_bX_c of a point X. This give us the triangle X'_aX'_bX'_c. Reflect the triangle
X'_aX'_bX'_c around sides of triangle ABC. Let [X_P] be the circumcircle of the triangle so formed.
P lies on the circle [X_P] if and only if X lies on the Lucas cubic.
Then, X_aX_bX_c is the pedal triangle of a point Y (on Darboux cubic) and Y is the center of [X_P].
On June, 10, 2014, I posed a problem at ADGEOM, which was generalized by Angel Montesdeoca in the following form:
Let ABC be a triangle. Let P be an arbitrary point on the plane of ABC. Reflect P around the vertices of cevian triangle X_aX_bX_c of a point X. This give us the triangle X'_aX'_bX'_c. Reflect the triangle
X'_aX'_bX'_c around sides of triangle ABC. Let [X_P] be the circumcircle of the triangle so formed.
P lies on the circle [X_P] if and only if X lies on the Lucas cubic.
Then, X_aX_bX_c is the pedal triangle of a point Y (on Darboux cubic) and Y is the center of [X_P].
miércoles, 1 de octubre de 2014
Concurrent Circles
Let ABC be a triangle.
Let P be a point on the plane of ABC.
Let a, b, c, are the sides opposite vertices A, B, C.
Let P_a be the reflection of P around the perpendicular
bisector of a. Define P_b, P_c cyclically.
Then, circles (AP_bP_c), (BP_aP_c), (CP_aP_b) are concurrent at
the circumcircle of ABC.
Let P be a point on the plane of ABC.
Let a, b, c, are the sides opposite vertices A, B, C.
Let P_a be the reflection of P around the perpendicular
bisector of a. Define P_b, P_c cyclically.
Then, circles (AP_bP_c), (BP_aP_c), (CP_aP_b) are concurrent at
the circumcircle of ABC.
martes, 26 de agosto de 2014
martes, 5 de agosto de 2014
Circumbicevian Perspector
Here's another point associated to cevians. I have dubbed it "Circumbicevian" perspector.
Description and proof
sábado, 2 de agosto de 2014
lunes, 21 de julio de 2014
viernes, 18 de julio de 2014
miércoles, 16 de julio de 2014
viernes, 4 de julio de 2014
domingo, 15 de junio de 2014
Garcia's Archimedean Quadruplets
One of the properties of the arbelos noticed and proved by Archimedes in his Book of Lemmas is that the two small circles inscribed into two pieces of the arbelos cut off by the line perpendicular to the base through the common point of the two small semicircles are equal. The circles have been known as Archimedes' Twin Circles. More than 2200 years after Archimedes,L. Bankoff (1974) has found another circle equal to the twins. In 1999 a large number of additional circles of the same radius has been reported by Dodge et al. More recently,F. Power described another quadruplet of circles that should be adopted into the family (Taken from CTK). In this page I am adding more circles.
For a description, please, go to Cut-The-Knot.org
Related topics:
Arbelos
Archimedes' Twin Circles
Archimedes' s Quadruplets
Bankoff Circle
Schoch Circles
Schoch Line
A Dozen More Arbelos Twins
Thomas Schoch - My Arbelos Story
Woo Circles
Online Catalogue of Archimedean Circles
miércoles, 11 de junio de 2014
Reductio ad absurdum beautifuly used
Theorem:
Not all problems can be solved.
Proof:
Suppose all problems can be solved (1).
We consider following problem P:
“To find one problem which can not be solved”
Because all problems can be solved therefore we can not find this problem. It means problem P can not be solved. It contradict (1) therefore “not all problems can be solved”.
The theorem is proved.
By Quang Tuan Bui
Not all problems can be solved.
Proof:
Suppose all problems can be solved (1).
We consider following problem P:
“To find one problem which can not be solved”
Because all problems can be solved therefore we can not find this problem. It means problem P can not be solved. It contradict (1) therefore “not all problems can be solved”.
The theorem is proved.
By Quang Tuan Bui
viernes, 6 de junio de 2014
martes, 3 de junio de 2014
The Cross-Touch Perspector
On Novermber, 2013, I discovered this point and inmediately sent it to Clark Kimberling and Peter Moses. The point is not listed on ETC, but, seemingly, has not special properties.
The configuration consist in a triangle with three semi-circles on each side and three common tangents lines. Now from each vertice draw a line joining the farthest tangenticial point on its corresponding semicircle and cyclic. The three intersecting points form a triangle wich is in perspective with the reference triangle.
I sometimes donate my results to AoPS when they have no special interest out of problem-solving, so I did. Next day, someone under the nick "Lyub4o" posted a proof which you can see here.
The internal version is the incenter of the reference triangle. I will take the liberty to name the external point "The Cross-Touch Perspector".
The configuration consist in a triangle with three semi-circles on each side and three common tangents lines. Now from each vertice draw a line joining the farthest tangenticial point on its corresponding semicircle and cyclic. The three intersecting points form a triangle wich is in perspective with the reference triangle.
I sometimes donate my results to AoPS when they have no special interest out of problem-solving, so I did. Next day, someone under the nick "Lyub4o" posted a proof which you can see here.
The internal version is the incenter of the reference triangle. I will take the liberty to name the external point "The Cross-Touch Perspector".
viernes, 28 de marzo de 2014
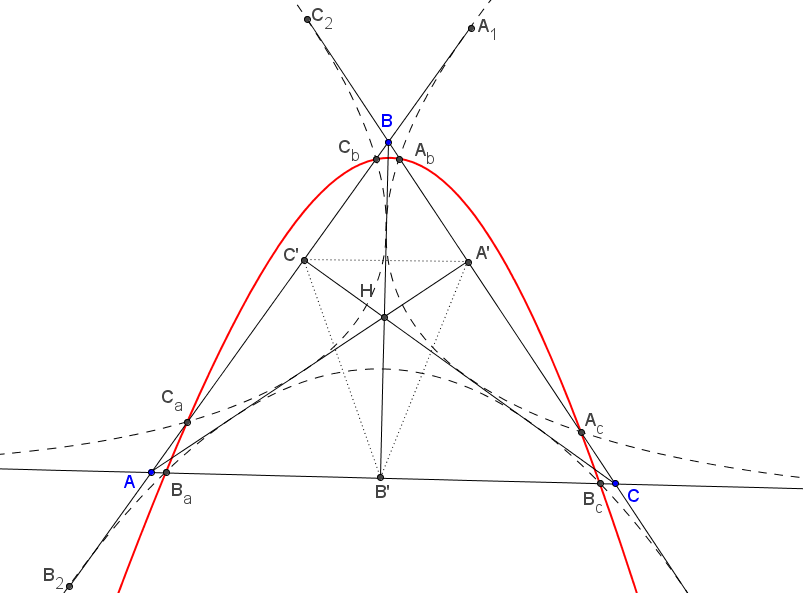
Some Properties of the Orthic Triangle - Conics
Let $ABC$ be a triangle. Let $A'B'C'$ be the orthic triangle of $ABC$. Draw a parabola focus at $A'$, directrix $B'C'$. Then, the parabola touches $BB'$ in $T_b$, $CC'$ in $T_c$, $AB$ in $A_1$ and $AC$ in $A_2$.
Proof:
Consider the following configuration:
Now it is easy to see why $BB'$, $CC'$ are tangent to the parabola.
We know that the orthocenter of $ABC$ is the incenter of the orthic triangle $A'B'C'$.
The tangency of $AB$ and $AC$ with the parabola follows directly from the Orthoptic property.
Addendum:
*Define $B_1$, $B_2$, $C_1$, $C_2$ as we define $A_1$, $A_2$.
Then, $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$ lie on a conic.
**Let the parabola cut the side $BC$ in $A_b$, $A_c$. Define $B_a$, $B_c$, $C_a$, $C_b$ cyclically. Then, these six points also lie on a conic.
Proof
domingo, 16 de marzo de 2014
Great Mathematicians on Math Competitions and "Genius"
As I mentioned in Fields Medalists on School Mathematics, school mathematics usually gives a heavily distorted picture of mathematical practice. It's common for bright young people to participate in math competitions, an activity which is closer to that of mathematical practice. Unfortunately, while math competitions may be more representative of mathematical practice than school mathematics, math competitions are themselves greatly misleading. Furthermore, they've become tied to a misleading mythological conception of "genius." I've collected relevant quotations below.
In a 2003 interview, Fields Medalist Terence Tao answered the question
What advice would you give to young people starting out in math (i.e. high school students and young researchers)?
by saying
Well, I guess they should be warned that their impressions of what professional mathematics is may be quite different from the reality. In elementary school I had the vague idea that professional mathematicians spent their time computing digits of pi, for instance, or perhaps devising and then solving Math Olympiad style problems.
In The Case against the Mathematical Tripos mathematician GH Hardy wrote
It has often been said that Tripos mathematics was a collection of elaborate futilities, and the accusation is broadly true. My own opinion is that this is the inevitable result, in a mathematical examination, of high standards and traditions. The examiner is not allowed to content himself with testing the competence and the knowledge of the candidates; his instructions are to provide a test of more than that, of initiative, imagination, and even of some sort of originality. And as there is only one test of originality in mathematics, namely the accomplishment of original work, and as it is useless to ask a youth of twenty-two to perform original research under examination conditions, the examination necessarily degenerates into a kind of game, and instruction for it into initiation into a series of stunts and tricks.
In The Map of My Life mathematician Goro Shimura wrote of his experience teaching at a cram school
I discovered that many of the exam problems were artificial and required some clever tricks. I avoided such types, and chose more straightforward problems, which one could solve with standard techniques and basic knowledge. There is a competition called the Mathematical Olympic, in which a competitor is asked to solve some problems, which are difficult and of the type I avoided. Though such a competition may have its raison d'être, I think those younger people who are seriously interested in mathematics will lose nothing by ignoring it.
In his lecture at the 2001 International Mathematics Olympiad, Andrew Wiles gave further description of how math competitions are unrepresentative of mathematical practice
Let me then welcome you not only to this event but also to the greater world of mathematics in what many of us believe is now a golden age. However let me also warn you — whatever the route you have taken so far, the real challenges of mathematics are still before you. I hope to give you a glimpse of this. What then distinguishes the mathematics we professional mathematicians do from the mathematical problems you have faced in the last week? The two principal differences I believe are of scale and novelty. First of scale: in a mathematics contest such as the one you have just entered, you are competing against time and against each other. While there have been periods, notably in the thirteenth, fourteenth and fifteenth centuries when mathematicians would engage in timed duels with each other, nowadays this is not the custom. In fact time is very much on your side. However the transition from a sprint to a marathon requires a new kind of stamina and a profoundly different test of character. We admire someone who can win a gold medal in five successive Olympics games not so much for the raw talent as for the strength of will and determination to pursue a goal over such a sustained period of time. Real mathematical theorems will require the same stamina whether you measure the effort in months or in years [...]
The second principal difference is one of novelty [...] Let me stress that creating new mathematics is a quite different occupation from solving problems in a contest. Why is this? Because you don't know for sure what you are trying to prove or indeed whether it is true.
In his Mathematical Education essay, Fields Medalist William Thurston said
Related to precociousness is the popular tendency to think of mathematics as a race or as an athletic competition. There are widespread high school math leagues: teams from regional high schools meet periodically and are given several problems, with an hour or so to solve them.
There are also state, national and international competitions. These competitions are fun, interesting, and educationally effective for the people who are successful in them. But they also have a downside. The competitions reinforce the notion that either you ‘have good math genes’, or you do not. They put an emphasis on being quick, at the expense of being deep and thoughtful. They emphasize questions which are puzzles with some hidden trick, rather than more realistic problems where a systematic and persistent approach is important. This discourages many people who are not as quick or as practiced, but might be good at working through problems when they have the time to think through them. Some of the best performers on the contests do become good mathematicians, but there are also many top mathematicians who were not so good on contest math.
Quickness is helpful in mathematics, but it is only one of the qualities which is helpful. For people who do not become mathematicians, the skills of contest math are probably even less relevant. These contests are a bit like spelling bees. There is some connection between good spelling and good writing, but the winner of the state spelling bee does not necessarily have the talent to become a good writer, and some fine writers are not good spellers. If there was a popular confusion between good spelling and good writing, many potential writers would be unnecessarily discouraged.
In his book Mathematics: A Very Short Introduction, Fields Medalist Timothy Gowers writes
While the negative portrayal of mathematicians may be damaging, by putting off people who would otherwise enjoy the subject and be good at it, the damage done by the word genius is more insidious and possibly greater. Here is a rough and ready definition of genius: somebody who can do easily, and at a young age, something that almost nobody else can do except after years of practice, if at all. The achievements of geniuses have some sort of magic quality about them - it is as if their brains work not just more efficiently than ours, but in a completely different way. Every year or two a mathematics undergraduate arrives at Cambridge who regularly manages to solve a in a few minutes problems that take most people, including those who are supposed to be teaching them, several hours or more. When faced with such a person, all one can do is stand back and admire.
And yet, these extraordinary people are not always the most successful research mathematicians. If you want to solve a problem that other professional mathematicians have tried and failed to solve before you, then, of the many qualities you will need, genius as I have defined it is neither necessary nor sufficient. To illustrate with an extreme example, Andrew Wiles, who (at the age of just over forty) proved Fermat's Last Theorem (which states that if x, y, z, and n are all positive integers and n is greater than 2, then xn + yn cannot equal zn) and thereby solved the world's most famous unsolved mathematics problem, is undoubtedly very clever, but he is not a genius in my sense.
How, you might ask, could he possibly have done what he did without some sort of mysterious extra brainpower? The answer is that, remarkable though his achievement was, it is not so remarkable as to defy explanation. I do not know precisely what enabled him to succeed, but he would have needed great courage, determination, and patience, a wide knowledge of some very difficult work done by others, the good fortune to be in the right mathematical area at the right time, and an exceptional strategic ability.
This last quality is, ultimately, more important than freakish mental speed: the most profound contributions to mathematics are often made by tortoises rather than hares. As mathematicians develop, they learn various tricks of the trade, partly from the work of other mathematicians and partly as a result of many hours spent thinking about mathematics. What determines whether they can use their expertise to solve notorious problems is, in large measure, a matter of careful planning: attempting problems that are likely to be fruitful, knowing when to give up a line of thought (a difficult judgement to make), being able to sketch broad outlines of arguments before, just occasionally, managing to fill in the details. This demands a level of maturity which is by no means incompatible with genius but which does not always accompany it.
In Does one have to be a genius to do maths? Terence Tao concurs with Gowers and expands on the same theme.
Fields Medalist Alexander Grothendieck describes his own relevant experience in Récoltes et Semailles
Since then I’ve had the chance in the world of mathematics that bid me welcome, to meet quite a number of people, both among my “elders” and among young people in my general age group who were more brilliant, much more ‘gifted’ than I was. I admired the facility with which they picked up, as if at play, new ideas, juggling them as if familiar with them from the cradle–while for myself I felt clumsy, even oafish, wandering painfully up an arduous track, like a dumb ox faced with an amorphous mountain of things I had to learn (so I was assured) things I felt incapable of understanding the essentials or following through to the end. Indeed, there was little about me that identified the kind of bright student who wins at prestigious competitions or assimilates almost by sleight of hand, the most forbidding subjects.
In fact, most of these comrades who I gauged to be more brilliant than I have gone on to become distinguished mathematicians. Still from the perspective or thirty or thirty five years, I can state that their imprint upon the mathematics of our time has not been very profound. They’ve done all things, often beautiful things in a context that was already set out before them, which they had no inclination to disturb. Without being aware of it, they’ve remained prisoners of those invisible and despotic circles which delimit the universe of a certain milieu in a given era. To have broken these bounds they would have to rediscover in themselves that capability which was their birthright, as it was mine: The capacity to be alone.
Source
Two Perspectors Are Collinear with the Incenter (Open problem)
Let ABC be a triangle. Let A', B', C' be the touch points of its incircle. Draw two internal semicircles with diameter BC', AC' & cyclic. Let semicircles BC', AC' meet the incircle in X, X', respectively. Define YY', ZZ' cyclically. Now the segments XX',YY', ZZ' form the triangle A_1, B_1, C_1. Also, let
B'' be the second intersection of semicircles BC', BA'. Define A'', C'' cyclically.
Then,
1) ABC is in perspective with A''B''C'' (in the incenter). This is trivial.
2) ABC is in perspective with A_1B_1C_1.
3) A''B''C'' is in perspective with A_1B_1C_1.
4) The three perspectors are collinear.
For more information see ADGEOM 1155
B'' be the second intersection of semicircles BC', BA'. Define A'', C'' cyclically.
Then,
1) ABC is in perspective with A''B''C'' (in the incenter). This is trivial.
2) ABC is in perspective with A_1B_1C_1.
3) A''B''C'' is in perspective with A_1B_1C_1.
4) The three perspectors are collinear.
For more information see ADGEOM 1155
sábado, 15 de marzo de 2014
Grebe-orthic perspector generalized
On Feb 15, 2003, Darij Grinberg published a new result (Grebe-orthic perspector) associated to the Grebe Triangle here. A generalization of this is given in this post.
For more information you can visit Angel Montesdeoca's Site (Jan 30, 2014).
Let ABC be a triangle. Let AB = a, BC = b, AC = c.
Let x, y, z be three distances from the sides of triangle ABC to the sides of triangle A'B'C', such that x/a = y/b = z/c.
Prove that the triangle A'B'C' is in perspective with the orthic triangle of ABC.
The proof at AoPS is due to Luís González.
For more information you can visit Angel Montesdeoca's Site (Jan 30, 2014).
Let ABC be a triangle. Let AB = a, BC = b, AC = c.
Let x, y, z be three distances from the sides of triangle ABC to the sides of triangle A'B'C', such that x/a = y/b = z/c.
Prove that the triangle A'B'C' is in perspective with the orthic triangle of ABC.
viernes, 14 de marzo de 2014
Two Triples of Concurrent Cevians and a Conic
In a triangle there are two pairs of concurrent cevians that - between them - have six feet on the side lines of a triangle.
Prove that there is a conic through all six points.
My proof is given in the comment section Cut The Knot
Prove that there is a conic through all six points.
My proof is given in the comment section Cut The Knot
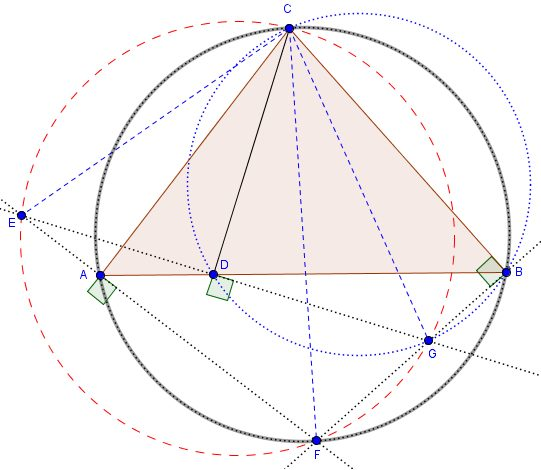
Concyclicity
$\triangle{ABC}$ is a triangle and $CD$ is its cevian. Draw perpendicular lines to $AC$, $CD$, $BC$ in $A$, $D$, $B$, respectively, such that they intersect at $E$, $F$, $G$. (See image)
Then $CEFG$ is cyclic.
Proof:
Since $\angle{CDG} = \angle{CBG} = 90^\circ$, then $CBDG$ is cyclic. Also, $\angle{CAF} = \angle{CBF} = 90^\circ$, then $ABCF$ is cyclic. Note that chord $CD$ is subtended both angles $\angle{CBD}$, $\angle{CGD}$ so $\angle{CBD} = \angle{CGD}$. Analogously, chord $AC$ is subtended by both angles, $\angle{CBD}$, $\angle{AFC}$ so $\angle{CBD} = \angle{AFC}$, then it follows that $\angle{AFC} = \angle{CGD}$. Note that $CE$ is subtended by both $\angle{AFC}$ and $\angle{CGD}$, hence $CEFG$ is cyclic.
Then $CEFG$ is cyclic.
Proof:
Since $\angle{CDG} = \angle{CBG} = 90^\circ$, then $CBDG$ is cyclic. Also, $\angle{CAF} = \angle{CBF} = 90^\circ$, then $ABCF$ is cyclic. Note that chord $CD$ is subtended both angles $\angle{CBD}$, $\angle{CGD}$ so $\angle{CBD} = \angle{CGD}$. Analogously, chord $AC$ is subtended by both angles, $\angle{CBD}$, $\angle{AFC}$ so $\angle{CBD} = \angle{AFC}$, then it follows that $\angle{AFC} = \angle{CGD}$. Note that $CE$ is subtended by both $\angle{AFC}$ and $\angle{CGD}$, hence $CEFG$ is cyclic.
Concyclicity (Proposed by Dao Thanh Oai)
$B$, $D$, $C$ are collinear. $A$ is another point on the plane. Draw $AB$, $AD$, $AC$, as in the figure. Rotate $AB$, $AD$, $AC$ from $B$, $D$, $C$ (couter clockwise or clockwise) the same angle. $\angle{EBA} = \angle{EDA} = \angle{FCA}$. $BE$ meets $CF$ in $F$; $DE$ meets $CF$ in $G$; $BE$ meets $DE$ in $E$.
Prove that $AEFG$ is cyclic.
Proof:
$\angle{EBA} = \angle{EDA} = \angle{FCA}$. The chord $EA$ is subtended by both angles $\angle{EBA}$, $\angle{EDA}$, so $ABDE$ is cyclic. Also, chord $AF$ is subtended by both angles $\angle{FBA}$, $\angle{FCA}$, so $ABCF$ is cyclic. Chord $AD$ is subtended by both angles $\angle{AED}$, $\angle{ABD}$. As $ABDE$ is cyclic $\angle{AED} = \angle{ABD}$. Chord $AC$ is subtended by both angles $\angle{AFC}$, $\angle{ABC}$. As $ABCF$ is cyclic $\angle{AFC} = \angle{ABC}$. Hence $\angle{AEG} = \angle{AFG}$. Indeed because the chord $AG$ is subtended by both angles $\angle{AEG}$, $\angle{AFG}$. Of course, this implies $AEFG$ is cyclic.
$Q.E.D.$
Garcia-Feuerbach Point
*Three congruent circles.
*All tangencies are obvious.
*DEF is a triangle in which G, H, I are touch points.
AH, CG, BI concur.
Also,
See X(5550)
*All tangencies are obvious.
*DEF is a triangle in which G, H, I are touch points.
AH, CG, BI concur.
Also,
See X(5550)
Garcia Point
*Three congruent circles.
*All tangencies are obvious.
*DEF is a triangle in which G, H, I are midpoints.
Prove that AH, CG, BI are concurrent.
Also,
See X(5550)
*All tangencies are obvious.
*DEF is a triangle in which G, H, I are midpoints.
Prove that AH, CG, BI are concurrent.
Also,
See X(5550)
jueves, 13 de marzo de 2014
Conic Associated to Three Parabolas and a Triangle
Let ABC be a triangle.
Let B and side AC be the focus and directrix of a parabola.
Let C and side AB be the focus and directrix of a parabola.
Let A and side BC be the focus and directrix of a parabola.
Let the black parabola intersect sides AB, BC in D, I respectively.
Let the blue parabola intersect sides AB, AC in E, F respectively.
Let the red parabola intersect sides AC, BC in G, H respectively.
Then, E, I, D, F, G, H lie on a conic.
Proof:
Proof:
AA', BB' CC' be the three altitudes
From the definition of parabola we have:
BD = DL; AF = FN; CH = HJ; BI = IM; CG = GK; AE = EO
By similarity we have:
BD = BB'*AD/AB
BE = AE*AB/AA'
AF = AA'*CF/AC
AG = CG*AC/CC'
CH = CC'*BH/BC
CI = BI*BC/BB'
From the Carnot's Theorem for conics:
BD*BE*AF*AG*CH*CI =
(BB'*AD/AB)(AE*AB/
So done.
Generalization
Let B and side AC be the focus and directrix of a parabola.
Let C and side AB be the focus and directrix of a parabola.
Let A and side BC be the focus and directrix of a parabola.
Let the black parabola intersect sides AB, BC in D, I respectively.
Let the blue parabola intersect sides AB, AC in E, F respectively.
Let the red parabola intersect sides AC, BC in G, H respectively.
Then, E, I, D, F, G, H lie on a conic.
Proof:
AA', BB' CC' be the three altitudes
From the definition of parabola we have:
BD = DL; AF = FN; CH = HJ; BI = IM; CG = GK; AE = EO
By similarity we have:
BD = BB'*AD/AB
BE = AE*AB/AA'
AF = AA'*CF/AC
AG = CG*AC/CC'
CH = CC'*BH/BC
CI = BI*BC/BB'
From the Carnot's Theorem for conics:
BD*BE*AF*AG*CH*CI =
(BB'*AD/AB)(AE*AB/
So done.
Generalization
Praying Eyes Theorem
A 3D view
As in the Eyeball theorem, the Praying Eyes variant seems to admit a generalization in 3D. Turn circles (A), (C) into spheres and line GH into a plane perpendicular to the plane of circles (A) and (C). The intersections of the plane (in green) and the two spheres are two congruent circles.
Related topics
Suscribirse a:
Entradas (Atom)