Concyclicity

$\triangle{ABC}$ is a triangle and $CD$ is its cevian. Draw perpendicular lines to $AC$, $CD$, $BC$ in $A$, $D$, $B$, respectively, such that they intersect at $E$, $F$, $G$. (See image)



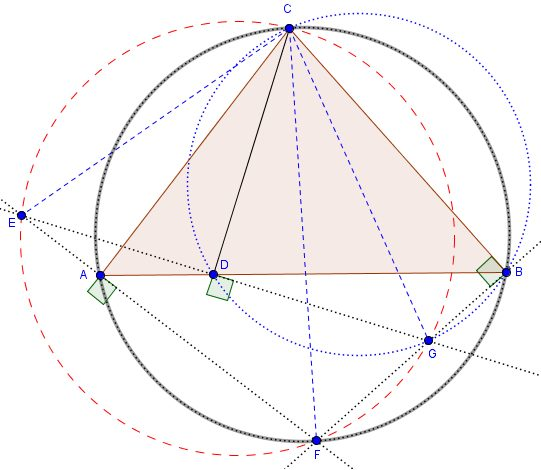
Then $CEFG$ is cyclic.

Proof:

Since $\angle{CDG} = \angle{CBG} = 90^\circ$, then $CBDG$ is cyclic. Also, $\angle{CAF} = \angle{CBF} = 90^\circ$, then $ABCF$ is cyclic. Note that chord $CD$ is subtended both angles $\angle{CBD}$, $\angle{CGD}$ so $\angle{CBD} = \angle{CGD}$. Analogously, chord $AC$ is subtended by both angles, $\angle{CBD}$, $\angle{AFC}$ so $\angle{CBD} = \angle{AFC}$, then it follows that $\angle{AFC} = \angle{CGD}$. Note that $CE$ is subtended by both $\angle{AFC}$ and $\angle{CGD}$, hence $CEFG$ is cyclic.