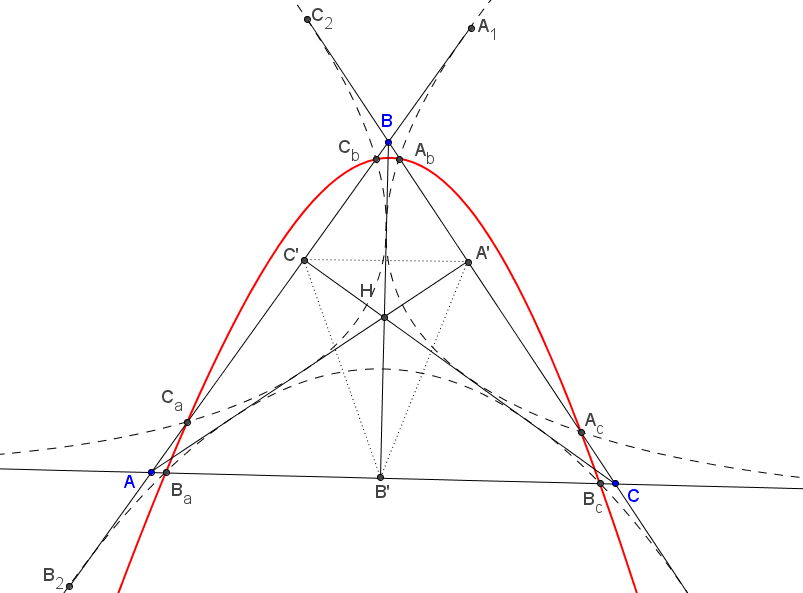
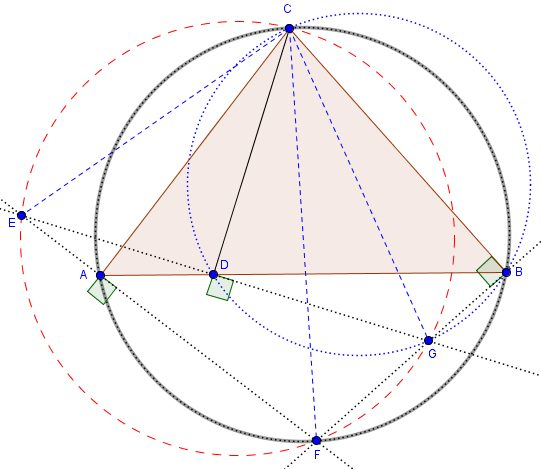
Let $\triangle ABC$ be a triangle. For each vertex take the corresponding opposite side as a directrix and the vertex as a focus, thus defining three parabolas:
the black parabola with focus $B$ and directrix $AC$,
the blue parabola with focus $C$ and directrix $AB$,
the red parabola with focus $A$ and directrix $BC$.
Let the black parabola meet $AB$ and $BC$ at $D$ and $I$, respectively.
Let the blue parabola meet $AB$ and $AC$ at $E$ and $F$, respectively.
Let the red parabola meet $AC$ and $BC$ at $G$ and $H$, respectively.
Then the six points $E,I,D,F,G,H$ lie on a conic.

Proof. Let $AA',BB',CC'$ denote the altitudes of $\triangle ABC$ (so $A'\in BC$, $B'\in AC$, $C'\in AB$).
For each point of intersection with a side, let the perpendicular foot from that point to the corresponding directrix be labelled as follows:
\[\begin{array}{c@{\qquad}c}\text{for }D\in AB: & L \text{ is the foot from }D\text{ to }AC,\\[4pt]\text{for }E\in AB: & O \text{ is the foot from }E\text{ to }BC,\\[4pt]\text{for }F\in AC: & N \text{ is the foot from }F\text{ to }BC,\\[4pt]
\text{for }G\in AC: & K \text{ is the foot from }G\text{ to }AB,\\[4pt]\text{for }H\in BC: & J \text{ is the foot from }H\text{ to }AB,\\[4pt]\text{for }I\in BC: & M \text{ is the foot from }I\text{ to }AC.\end{array}\]
By the definition of a parabola (distance to focus equals distance to directrix) we have the six equalities
\begin{equation}\label{parab:eqs}
BD = DL,\quad AE = EO,\quad AF = FN,\quad CG = GK,\quad CH = HJ,\quad BI = IM.
\end{equation}
By similarity of appropriate right triangles (using the altitudes $AA',BB',CC'$) we obtain the relations
\begin{align}
BD &= \frac{BB'}{AB}\,AD, &
BE &= \frac{AE}{AA'}\,AB, \label{sim:1}\\
AF &= \frac{AA'}{AC}\,CF, &
AG &= \frac{CG}{CC'}\,AC, \label{sim:2}\\
CH &= \frac{CC'}{BC}\,BH, &
CI &= \frac{BI}{BB'}\,BC. \label{sim:3}
\end{align}
(Each of the above equalities is the result of comparing similar right triangles formed by an altitude and the corresponding distances along the sides.)
Consider the product
\[BD\cdot BE\cdot AF\cdot AG\cdot CH\cdot CI.\]
Substituting the expressions yields
\[\begin{aligned}BD\cdot BE\cdot AF\cdot AG\cdot CH\cdot CI
&= \left(\frac{BB'}{AB}AD\right)\left(\frac{AE}{AA'}AB\right)\left(\frac{AA'}{AC}CF\right) \\
&\qquad\cdot\left(\frac{CG}{CC'}AC\right)\left(\frac{CC'}{BC}BH\right)\left(\frac{BI}{BB'}BC\right) \\
&= AD\cdot AE\cdot CF\cdot CG\cdot BH\cdot BI.
\end{aligned}\]
By the Carnot criterion for six points to lie on a (nondegenerate) conic (often stated in the form that a certain product of directed segment lengths is equal), the equality
\[BD\cdot BE\cdot AF\cdot AG\cdot CH\cdot CI = AD\cdot AE\cdot CF\cdot CG\cdot BH\cdot BI\]
is exactly the required multiplicative relation. Hence the six points $E,I,D,F,G,H$ lie on a conic.