Solution of a problem by Tran Viet Hung

 This is problem $037$ in this document by the Vietnamese geometer, Tran Viet Hung. 

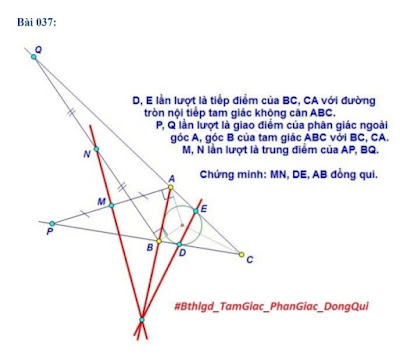
Problem. Let $ABC$ be a triangle and $I$ its Incenter. Denote $D$, $E$ the points of tangency of incircle of $ABC$ with sides $BC$ and $AC$, respectively. Let $P$ be the intersection of the perpendicular of $AI$ at $A$ and $BC$. Construct $Q$ similarly. Denote $M$ and $N$ the midpoints of $AP$ and $BQ$, respectively. Prove that $MN$, $AB$ and $DE$ concur (see figure below). 

Lemma 1. Let $P'$ be the intersection of $AI$ with $BC$ and $Q'$ the intersection of $BI$ with $AC$. Denote $M'$ and $N'$ the midpoints of $AP'$ and $BQ'$, respectively. Call $X$ the intersection of $AN'$ with $BM'$. If $T'$ is the point of tangency of the $C$-excircle with $AB$, then $T'$, $X$ and $I$ are collinear. 

Proof. Here we'll be using standard notations, this is $BC=a$, $AC=b$, $AB=c$ and $s$ is semiperimeter. From the formula for the length of angle bisector we have

$$AP'=\frac{2\sqrt{bcs(s-a)}}{b+c}.\tag{1}$$

Moreover, it is well-known that

$$AI=\sqrt{\frac{bc(s-a)}{s}}.\tag{2}$$

From $(1)$ and $(2)$ follows that

$$M'I=AI-\frac{AP'}{2}=\sqrt{\frac{bc(s-a)}{s}}-\frac{\sqrt{bcs(s-a)}}{b+c}=\frac{1}{b+c}\cdot{\sqrt{\frac{bc(s-a)^3}{s}}}.$$

Similarly, we can derive an expression for $N'I$, 

$$N'I=BI-\frac{BQ'}{2}=\sqrt{\frac{ac(s-b)}{s}}-\frac{\sqrt{acs(s-b)}}{a+c}=\frac{1}{a+c}\cdot{\sqrt{\frac{ac(s-b)^3}{s}}}.$$

Invoking Ceva's theorem, our goal now is to show that

$$\frac{AM'}{M'I}\cdot{\frac{N'I}{BN'}}\cdot{\frac{BT'}{AT'}}=1.\tag{3}$$

Since $AT'=(s-b)$ and $BT'=(s-a)$, equation $(3)$ can be re-written as

$$\frac{\sqrt{bcs(s-a)}}{\sqrt{\frac{bc(s-a)^3}{s}}}\cdot{\frac{\sqrt{\frac{ac(s-b)^3}{s}}}{\sqrt{acs(s-b)}}}\cdot{\frac{s-a}{s-b}}=\frac{s}{s-a}\cdot{\frac{s-b}{s}}\cdot{\frac{s-a}{s-b}}=1.$$

This means that $AN'$, $BM'$ and $IT'$ are concurrent at $X$. Hence $T'$, $X$ and $I$ must be collinear.

$\square$ 

Back to Hung's original problem

Call $I_c$ the $C$-excenter of $ABC$. By property of ex-centers, $\angle{IBI_c}=\angle{IAI_c}=90^\circ$, so $AP$ and $BQ$ must intersect at $I_c$. Denote $Y$ the intersection of $AN$ with $BM$ and $T$ the point of tangency of the incircle with $AB$. Then $Y$, $I_c$ and $T$ must be collinear since this is the extraverted version of Lemma 1. Now, suppose $DE$ and $MN$ intersect $AB$ at $R$ and $R'$, respectively. It is well-known that $AD$, $BE$ and $CT'$ are concurrent at the Gergonne Point, so by property of harmonic bundles we have

$$-1=(A, B; T, R)=(A, B; T, R'),$$

wich means $R=R'$, hence $MN$, $AB$ and $DE$ concur.

$\square$

Remark. Lemma 1 has given rise to a new special triangle, namely the Garcia-Moses triangle, published in the Encyclopedia of Triangle Centers.