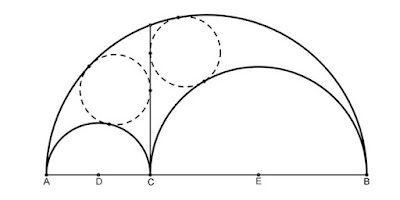
GeoDom: El Árbelos y esos Círculos Gemelos de Arquímedes

Antes de ir al móvil principal de este artículo, definamos qué es un árbelos. Árbelos es la figura formada por tres semicírculos mutuamente tangentes entre sí, con sus centros alineados. La palabra árbelos viene del griego άρβυλος, significando: cuchillo de zapatero.

Una de las propiedades del árbelos descubierta y probada por el mismo Arquímedes en su libro de lemas, es que los dos pequeños círculos inscritos en las regiones del árbelos cortadas por una línea perpendicular en la base a través del punto de contacto de los dos pequeños semicírculos, son iguales. Los círculos se han conocido desde entonces como los Círculos Gemelos de Arquímedes.

Más de 2200 años después de Arquímedes, Leon Bankoff (1974) encontró otro círculo congruente con los gemelos. En 1999, un gran número de círculos con igual radio fue reportado por C. W. Dodge. Más recientemente, F. Power describió otros cuatro círculos que fueron adoptados en la familia.

Muchas sorprendentes y contraintuitivas propiedades se han encontrado con relación a esta configuración. Hay quien sugiere que el hecho de que esta figura tan simple sea tan rica en propiedades, quizá, se deba a que el arbelos no es más que un triángulo cuyos lados son semicírculos.

En 1979, Martin Gardner escribió acerca del círculo trillizo de Bankoff, inspirando al entonces estudiante Thomas Schoch, de Essen, Alemania, a descubrir más círculos. Él envió su trabajo en alemán a Gardner, quién lo reenvió a Bankoff. Bankoff no estaba familiarizado con el idioma alemán, así que envió una copia a Dodge en 1996. Dodge reconoció la alta calidad del artículo de Schoch y salió de viaje tratando de localizarlo. Él, aún viviendo en Essen, no le había dado seguimiento a su trabajo hasta que encontró el sitio web de árbelos del Dr. Peter Woo, en 1998. Schoch contactó a Woo y le contó sobre sus hallazgos. Paul Yiu dirigió la atención de Dodge hacia Woo, quien había completado un artículo sobre sus infinitos círculos arquimedianos. Es entonces cuando deciden unir fuerzas para escribir un artículo: "Those Ubiquitous Archimedean Circles" (Aquellos ubicuos círculos arquimedianos). No puedo dejar de mencionar que Victor Thébault (el gran 'problemista' francés) estudió exhaustivamente el árbelos.

El interés en el árbelos sigue vigente en la comunidad Matemática. Como muestra, en 2004, Hiroshi Okumura y Masayuki Watanabe, del Instituto de Tecnología Maebashi (Japón), publicaron una generalización de los círculos arquimedianos de Woo y de Schoch. A partir del 2006, Floor van Lamoen descubrió más círculos y varias familias infinitas. En 2013, Hiroshi Okumura presentó una generalización avanzada del árbelos y sus círculos arquimedianos, y mostró los círculos generalizados cubriendo un plano.

El 15 de Junio del 2014, el autor de este artículo engrosó un poco más la familia (hay infinitas familias de círculos arquimedianos. Lo que en realidad hice fue aumentar el número de configuraciones donde podemos encontrar círculos de Arquímedes). Mientras hurgaba en la página de Alexander Bogomolny en busca de problemas sin demostración, encontré un problema no resuelto sobre tangencias y círculos cuya clave para su demostración consistía en un simple detalle de congruencia de triángulos. El problema guardaba similitud con un problema que yo había publicado y demostrado en 2013, resultando ser una variante aparentemente desconocida del famoso teorema Eyeball. En vista de este vínculo con el teorema Eyeball, Bogomolny tomó la libertad de apodarlo "The Praying Eyes Theorem". En ese momento no imaginaba que pudiera tener un vínculo con los gemelos de Arquímedes, pero una semana antes de escribir este artículo, había pasado algunas horas estudiando el Catálogo de Círculos Arquimedianos disponible en línea, y me preguntaba si podía haber alguna conexión. ¡Aja! Fue como un regalo de cumpleaños (justo el día anterior era mi cumpleaños). Vayamos a la descripción:

Los semicírculos (D) y (E) se dibujan sobre los diámetros AC y BC, respectivamente, siendo C un punto sobre el segmento AB. EF es tangente a (D) y DG es tangente a (E). La línea FG intersecta (D) por segunda vez en I y (E) enH. Los dos círculos en FI y GH como diámetros son gemelos arquimedianos (tienen el radio igual al par de círculos descubierto por Arquímedes).

Tanto la demostración como otros círculos adicionales correspondientes a esta configuración se detallan elegantemente en la sección de árbelos del website de Alexander Bogomolny.

¡Si tan sólo Arquímedes supiera!