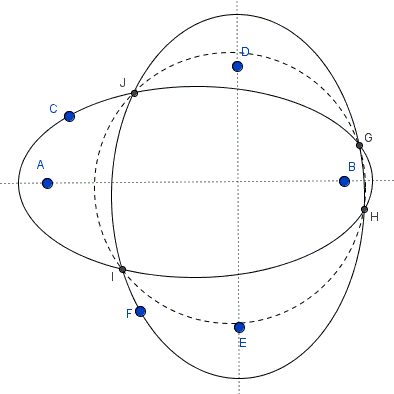
Consider an ellipse with foci $A$ and $B$. Let $C$ be the center of a circle tangent to the ellipse at $T$. From $A$, draw two tangents lines to the circle and let $A_1$, $A_2$ be the points where these tangents lines meet the ellipse. Similarly, define $B_1$ and $B_2$. Let $O$ be the intersection of $AA_1$ and $BB_1$. Let $P$ be the intersection of $AA_2$ and $BB_2$. Let $Q$ be the intersection of $AA_1$ and $BB_2$.
Prove that $O$, $P$ and $Q$ are collinear.