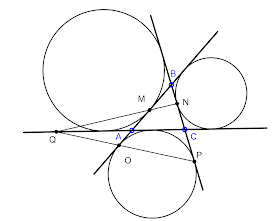
Problema 4. Sea $ABCD$ un trapecio con $AB\parallel{CD}$ e inscrito en la circunferencia $\tau$. Sean $P$ y $Q$ dos puntos en el segmento $AB$ ($A$, $P$, $Q$, $B$ están en ese orden y son distintos) tales que $AP=QB$. Sean $E$ y $F$ los segundos puntos de intersección de las rectas $CP$ Y $CQ$ con $\tau$, respectivamente. Las rectas $AB$ y $EF$ se cortan en $G$. Demuestre que la recta $DG$ es tangente a $\tau$.
Demostración. Suponga que la tangente que pasa por $D$ interseca a la recta $AB$ en $G$. Será suficiente probar que $G$, $E$ y $F$ están alineados. Si $GT$ es la otra tangente común a la circunferencia circunscrita de $ABCD$, entonces $DATB$ es un cuadrilátero armónico. Llamemos $M$ a la intersección de la recta $CT$ con $AB$. Proyectando desde $C$ sobre la recta $AB$, tenemos que $(A, B; T, D) = (A, B; M, P_\infty) = -1$, lo que implica que $CT$ pasa por el punto medio de $AB$. Como $AP = BQ$, $M$ es también el punto medio de $PQ$. Proyectando nuevamente desde $C$ sobre la circunferencia circunscrita de $ABCD$, tenemos que $(P, Q; M, P_\infty) = (E, F; T, D) = -1$. Por lo tanto, $G$, $E$ y $F$ están alineados.
$\square$