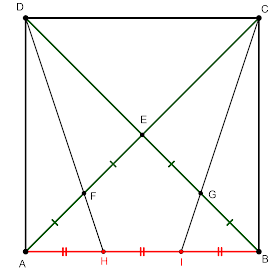
Let $E$ be the center of the square $ABCD$. Call $F$ the midpoint of $AE$ and let $DF$ meet $AB$ in $H$. Then, $AH=\frac{AB}{3}$.
Proof 1. We will set our origin at $A$, and side $AB$ of the square will lie on the $x$-axis. $A$ has coordinates $(0,0)$. $B$ has coordinates $(a, 0)$. $D$ has coordinates $(0, a)$. $E$ is the midpoint of $BD$ and has coordinates $(\frac{a}{2}, \frac{a}{2})$ and $F$ is the midpoint of $AE$ with coordinates $(\frac{a}{4}, \frac{a}{4})$. The equation of line $DF$ is $y=-3x+a$. Then, the intersection, $H$, of line $DF$ and $AB$ is $(\frac{a}{3}, 0)$. Therefore, $AH=\frac{AB}{3}$.
Proof 2. Denote by $a$, $b$, $c$ and $d$ the segments $AD$, $AH$, $FH$ and $DF$, respectively. Focusing on triangle $\triangle{ADE}$ and median $DF$, by the Apollonius's theorem,
$$a^2+\frac{a^2}{2}=2(\frac{a^2}{8}+d^2).$$
Solving for $d$,
$$d=\frac{a\sqrt{10}}{4}.$$
By the angle bisector theorem, $c=\frac{bd}{a}=\frac{b\sqrt{10}}{4}$. Now, by the Pythagorean theorem,
$$a^2+b^2=\left[\frac{\sqrt{10}}{4}(a+b)\right]^2.$$
Solving this equation for $b$ we get $b_1=3a; b_2=\frac{a}{3}$, but, from our configuration $a>b$, therefore, $b=\frac{a}{3}$.
Related material